Do you speak data?

Are you interested in telling data stories with data visualizations? But your data language can use some improvements? Maybe you are a beginner in the field or maybe you just want to brush up on your knowledge. Whatever the reason, you have come to the right place. In this article, we will explain the meaning of the most common terms in data and statistics that you might encounter when you are interested in creating data visualizations.
Table of content
1. Every data visualization begins with a dataset 2. Numerical and categorical variables 3. Data formats 4. Independent and dependent variables 9. References |
Every data visualization begins with a dataset
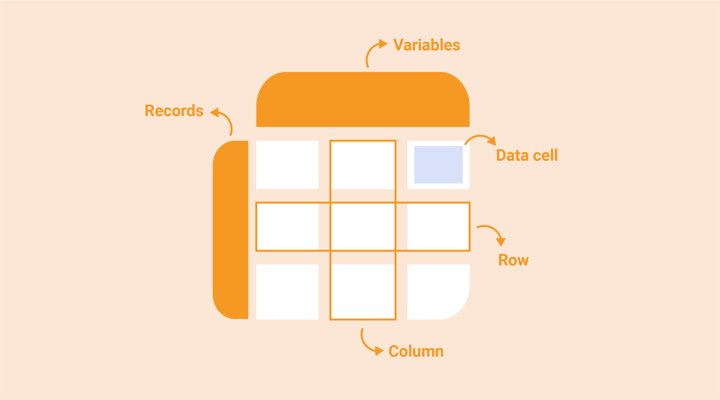
Let’s start from the beginning. If you wish to create any data visualization, you need a dataset. A dataset is a collection of data that is most often shown in a table consisting of rows (horizontal) and columns (vertical). In every box or data cell, information can be stored. Generally, the columns represent variables and each row represents a record.
To easily manage your data, you can make use of workbooks containing worksheets or spreadsheets to store the data.
Numerical and categorical variables
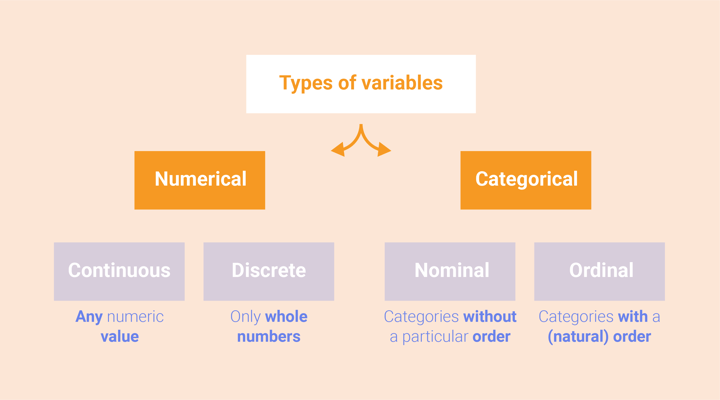
Variables can be categorized into numerical variables or categorical variables. Numerical variables can be anything that is in the form of a number and therefore you can make calculations with these variables.
There are two types of numerical variables:
- Continuous variables: variables that can take any value on any range, for example from 0.15 to 4627.625, to 15.2, or to 163.0. Examples of continuous data are the temperature outside, the length of your foot, or the weight of a baby.
- Discrete variables: variables that involve whole numbers; numbers that you can count. This holds for example for the number of colleagues in your team or the number of items on your shopping list.
Categorical variables consist of information that can be categorized. Categorical variables can be subdivided into:
- Nominal variables: variables that can be categorized without a particular order, such as gender or eye color.
- Ordinal variables: variables that are categorical and can be ordered in a natural way, such as income level or level of satisfaction.
These types of variables can be really important when it comes to data visualization. Some types of charts are more suitable for specific types of variables. For example, we recommend using a bar chart for categorical data without a natural order. On the other hand, data with a natural order will be better represented by a column chart.
Data formats
Now that you know how to categorize the variables, it is also important to match the specific data format. This will help in managing your data and being able to do calculations and perform operations on the variables1.
There are different types of data formats and we will discuss the most important ones. Continuous numerical variables are often represented as floats. This type of data format is composed of a numerical value with decimals. Discrete numeric variables are often represented as integers, numbers that you can count. Nominal categorical variables will be shown as strings, values that are treated as texts. And last, ordinal categorical variables will be represented as integers or strings. Categorical data can also be stored as a factor, which can be both integer or string. A factor includes several levels and the categories of the variable, and can be both ordered and unordered.
The type of variable we didn’t discuss yet is the binary variable. This is a type of categorical variable that can only take up one or two values. Often these are represented as boolean values: True or False, or as integers: 0 or 1.
Lastly, a common data format is the date time format. This type of format stores dates and times and this can be done in different ways, based on how the data looks like.
Independent and dependent variables
When creating data visualization, you have to decide which variables you will plot on the x-axis and which on the y-axis. Commonly, independent variables (or predictor variables) are plotted on the x-axis of the chart. This type of variable is the variable that is not dependent on other variables or is the one that is manipulated by the researcher in an experiment in order to find an effect on the dependent variable. The dependent variable (or response variable) is the variable that will be studied or measured and is therefore dependent on or a response to the independent variable. The dependent variable is most commonly plotted on the y-axis of a chart.

Sometimes there is a third variable that will influence the independent and dependent variable; the confounding variable. Considering the effects of such a variable is important when designing an experiment.
To give you more insights into the dependent and independent variables, I will show you an example of an experiment. For this experiment, a representative group from the population, also called a sample, is selected to participate in a running challenge. The group will be split into subgroups, also called conditions, and each group will receive a different type of energy drink. In this case, the type of energy drink will be the independent variable, or the variable that we manipulated. After consuming the energy drink, the participants will perform a running circuit and we will measure the total amount of time they spend completing the running circuit, their heartbeat during the challenge, and their heartbeat five minutes after they finish. You can guess, these variables will be the dependent variables.
The distribution
After we collected the data of our running experiment, each possible outcome for the variables we measured can be described in a distribution. There are a lot of types of distributions, but the most common one that you are probably familiar with is the normal distribution.
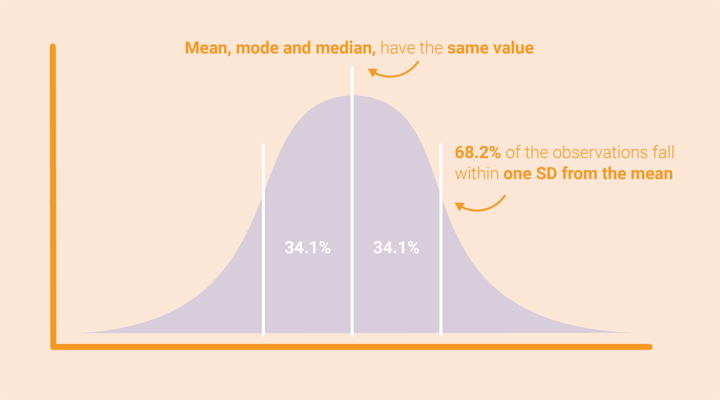
The normal distribution is a symmetric distribution around the mean; values close to the mean are more frequent and values far away from the mean are less frequent. The mean in the data is the same as the average of the data and can be calculated by adding all values and dividing them by the number of values in the data set. The standard deviation (SD) shows how dispersed the data is compared to the mean and therefore will determine the width of the distribution. In more mathematical terms; the standard deviation is the square root of the variance. And what is the variance, you might wonder. The variance is the mean squared difference between each number in the data set and the mean2.
The mean in a data set is a measurement of central tendency3, a summary measure to describe a whole data set with only one value. Other types of central tendency are the mode and median. The mode is the value that occurs the most in the dataset and the median is the middle number of the data set. Some values will have a lot of impact on some of these measurements of central tendency. Values that differ abnormally from the others are called outliers, and these outliers will affect the mean but will have less impact on the mode or median of the data set4. In a normal distribution, the mean, median, and mode all have the same value, and 68.2% of the observations will fall within around one standard deviation of the mean5.
Sometimes the distribution of your data is not as equally distributed as in a normal distribution and the distribution might have a longer tail on the left or right side. This is called skewness. When the distribution has a longer tail on the right, it is called right skewed, when it is longer on the left it is called left-skewed4.
Calculations with data
Besides describing the data with a measurement of central tendency, there are also some other ways to describe or do calculations on the data. A variant on the average is the moving average. This type of average is calculated by adding all data points in a specific time period and dividing it by the number of time periods. In this way, random fluctuations in the data are smoothed out.
Where the moving average shows the average value over a specific time period, cumulative values show the total so far. To find it, you can just add up all the data points there are so far.
Another way of doing calculations with data that you are probably familiar with is the ratio of data. The ratio is the same as the proportion and can be something like: the ratio between women and men in the tech industry is 1:4. You can also describe this differently by comparing the ratio with 100, which is called a percentage. In this case, the percentage will be 25% women and 75% men. A variant on percentage is percentage point. This value is the difference between two percentages. So if the data moves up from 50% to 55%, it moves up 5 percentage points but also a 10-percent increase. It is very important to know the difference between these two since you probably encounter these when creating data visualizations for companies.
Just like percentages, there is also another type of value that can never be negative; the absolute value. This type of value shows the distance of the value from zero.
Statistical tests
As discussed before, sometimes your variable doesn’t follow a normal distribution, which can be a problem if you are interested in performing statistical tests on them. You can perform a data transformation on those variables and normalize them to make sure they equally contribute to the analysis6. Therefore, always check before you perform a statistical test, what the assumptions are of this type of test and if you need to normalize the data or if there are alternatives.
When visualizing data, you sometimes want to show if some categories differ significantly from each other. Most often these differences in a chart are indicated with one or multiple stars (*). But what does a significant difference actually mean?
Analysts will perform a statistical test and they will find out that a relationship exists between variables, that is not caused by chance7. The test they perform will show a p-value which describes the probability that the result found is the result of chance, or in other words that the null hypothesis is true7. Common p-value thresholds used by researchers in the analysis are 0.05 or 0.001. So next time you have to add a p-value to your data visualization, you will know what it means.
Besides using stars (*) to indicate that groups significantly differ from each other, for scatter plots the p-value is mentioned in combination with the correlation coefficient, or “r”. The correlation coefficient is a statistical test that shows the correlation between the independent (predictor) and dependent (response) variable8.
The bigger picture
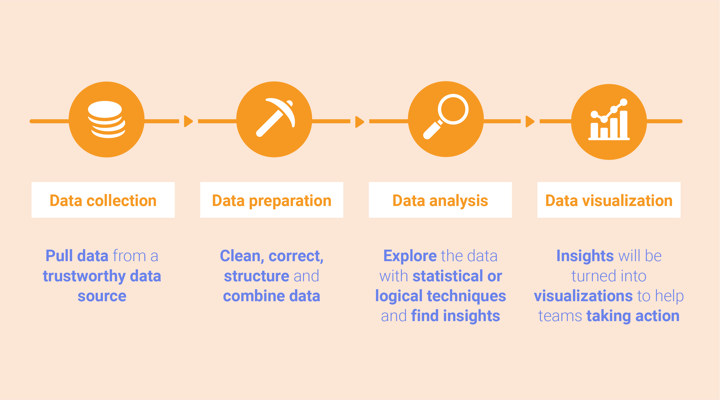
In this article, you learned a lot of terms that are used in the data and statistics field that might come in handy when you are interested in creating data visualization. Everything explained before in this article is all part of data analysis. However, there are also a lot more steps in the data process that are relevant to know for a data visualization designer. I will briefly discuss them so you will have a better understanding of the bigger picture of working with data.
The first step is data collection and this means that data is pulled from data sources. It is important to always check the quality and trustworthiness of the data source. Data collection can also be done by making use of an Application Programming Interface (API). As Amazon explained: “APIs are mechanisms that enable two software components to communicate with each other using a set of definitions and protocols.”
After that, the data preparation phase can start during which the data cleaning will happen. Here, the data will be checked for errors such as incorrect data formats, empty fields, or duplicate data. Moreover, in this step, the data can be structured or sorted, or data sets can be combined to make it easier to start the data analysis. This step is called data wrangling. Filters can also be applied to the data to select a subset of the data you are interested in for your analysis.
Thereafter the actual data analysis can begin, which often starts with data exploration. In this step visualizations or statistical methods are used to discover insights. During the analysis, data mining can also be done to discover and extract patterns by using machine learning, statistics, and database systems9.
Lastly, the data visualization phase can start in which insights will be turned into visualizations to help teams in their decision-making and taking action.
As you become more familiar with data analysis, you'll likely begin using a variety of tools to streamline your process. From spreadsheets—which are great for organizing and manipulating data—to statistical software, which helps perform complex analyses, and specialized data visualization tools that turn raw data into clear visual insights. These tools assist in exploring, analyzing, and presenting your findings.
But as your datasets grow and the need for timely insights increases, manually performing these tasks can become repetitive and time-consuming. This is where automated reporting tools can greatly enhance your workflow.
Automated reporting refers to the process of using software to automatically generate static charts and reports without needing to manually update them every time. These tools connect directly to your data sources—the systems or databases where your data is stored—and apply templates to format the reports consistently. A template is a predefined layout or structure that determines how your charts and data will appear in the final report, so you don’t have to start from scratch each time.
By using automated reporting, businesses and analysts can ensure that their reports are always up-to-date, error-free, and formatted in a consistent way. This not only saves time but also makes it easier to share insights regularly or in scheduled intervals, which can be critical when working with large teams or managing multiple projects.
Datylon Report Server simplifies the process of automating static charts and report generation. Simply design your template, connect to the data source, and effortlessly produce charts and reports on demand or according to a schedule. Schedule a demo today to experience the power of automated reporting firsthand.
References
1Variable types by Codeacademy.
2Standard Deviation vs. Variance: What's the Difference? by Investopedia.
3Mean Median Mode: What They Are, How to Find Them by Statistics How To.
4Central Tendency by Pennsylvania Department of Education.
5Normal Distribution by Investopedia.
6How, When, and Why Should You Normalize / Standardize / Rescale Your Data? by Towards AI.
7 Statistical Significance: What It Is, How It Works, With Examples by Investopedia.
8R vs. R-Squared: What’s the Difference? by Statology.
9Data mining by Wikipedia.

Dieuwertje van Dijk - Data Visualization Designer
Data, graphic design, illustration, food and mountains let her dopamine neurons spark on a daily basis. Most of the year she lives in Georgia where she spends her free time enjoying nature in a rooftop tent, eating khinkali and drinking wine.